Robust output regulation for autonomous robots

Abstract

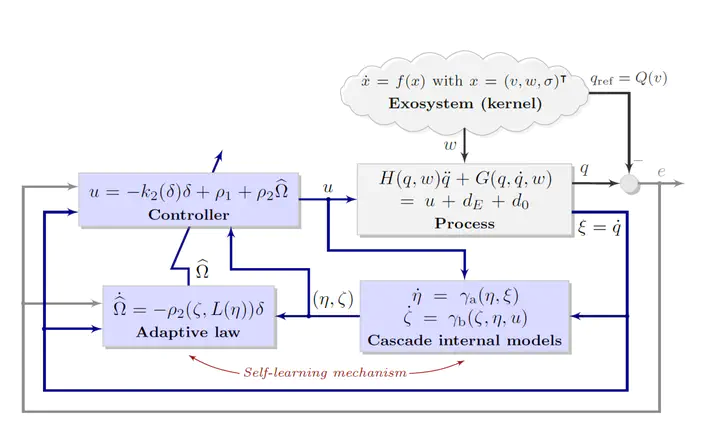
In this presentation the problem of robust output regulation for autonomous robots is studied. In general, the control objective of output regulation is to design a feedback controller to achieve asymptotic tracking and/or disturbance rejection for a class of exogenous reference and/or disturbance while maintaining closed-loop stability. Three research problems that pertain to the constructive design of robust output regulation for fully actuated Euler-Lagrange systems from centralized to distributed fashions. The first one is the global robust output regulation of second-order affine nonlinear systems with input disturbances that encompass the fully-actuated Euler-Lagrange systems. Based on a certainty equivalence principle method, we proposed a novel class of nonlinear internal models taking a cascade interconnection structure with strictly relaxed conditions than before. The second one is the output regulation for robot manipulators operating in task-space. An internal model-based adaptive controller is designed to cope with uncertain manipulator kinematic and dynamic parameters, as well as unknown periodic reference trajectories generated by harmonic oscillators. The last one is the formation control of manipulators end-effector subject to external disturbances or parameter uncertainties. We present and analyze gradient descent-based distributed formation controllers for end-effectors. Internal models are used to reject external disturbances. Moreover, by introducing an extra integrator and an adaptive estimator for gravitational compensation and stabilization, respectively, we extend the proposed gradient-based design to the case where the plant parameters are not exactly known.